The tetrahedron, cube, and octahedron all occur naturally in crystal structures. These by no means exhaust the numbers of possible forms of crystals. However, neither the regular icosahedron nor the regular dodecahedron are amongst them. One of the forms, called the pyritohedron (named for the group of minerals of which it is typical) has twelve pentagonal faces, arranged in the same pattern as the faces of the regular dodecahedron. The faces of the pyritohedron are, however, not regular, so the pyritohedron is also not regular.
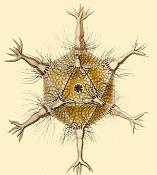
In the early 20th century, Ernst Haeckel described (Haeckel, 1904) a number of species of Radiolaria, some of whose skeletons are shaped like various regular polyhedra. Examples include Circoporus octahedrus, Circogonia icosahedra, Lithocubus geometricus and Circorrhegma dodecahedra. The shapes of these creatures should be obvious from their names.
Many viruses, such as the herpes virus, have the shape of a regular icosahedron. Viral structures are built of repeated identical protein subunits and the icosahedron is the easiest shape to assemble using these subunits. A regular polyhedron is used because it can be built from a single basic unit protein used over and over again; this saves space in the viral genome.
In meteorology and climatology, global numerical models of atmospheric flow are of increasing interest which employ grids that are based on an icosahedron (refined by triangulation) instead of the more commonly used longitude/latitude grid. This has the advantage of evenly distributed spatial resolution without singularities (i.e. the poles) at the expense of somewhat greater numerical difficulty.




No comments:
Post a Comment